Guía rápida y completa de Vectores (Nivel Fácil)
Los vectores son útiles para todo, desde orientar direcciones hasta realizar obras de arte. Los programas que usan gráficos vectoriales como Ilustrator e Inkscape se caracterizan por generar imágenes que no se despixelan lo cual los hace ideales para la elaboración de logotipos por encima de programas manipuladores de pixeles como el Photoshop y Gimp. Hoy hablaremos de vectores en forma básica, solo lo que necesitamos saber para hacer un poco de física.

Imagen creada con “gráficos vectoriales”
Vectores ¿qué son los pares ordenados?:
Antes de hablar de vectores, debemos hablar de “pares ordenados”, es decir, como expresar puntos en el plano XY (también llamado plano cartesiano). Un par ordenado (x,y) se representa en el plano cartesiano colocando un punto en el eje X a la altura que indicada en el eje Y.

Otra forma conveniente de representar un punto en el plano es usar las coordenadas polares. Donde debemos hallar un módulo “r” y un ángulo "theta" con la siguiente transformación:


Estas 4 expresiones relacionan las coordenadas cartesianas (x,y) con las coordenadas polares (r,theta)

Cantidades Escalares y Cantidades Vectoriales:
Ya que sabemos representar un punto en el plano en dos sistemas coordenados, podemos comenzar hablar de vectores y sus propiedades. Para ello vamos a definir:
Cantidad escalar:
Se entiende como una cantidad dada por un único valor con una unidad apropiada y que no posee dirección.Cantidad vectorial:
Esta posee magnitud, dirección y sentido.Ahora sí, podemos definir la palabra Vector; es un segmento de recta que posee modulo (magnitud), dirección y sentido. Donde la dirección es dada por el segmento de recta que lo contiene y la dirección puede ser tanto positiva como negativa respecto a un sistema de coordenadas dado.
Propiedades de los vectores en el plano cartesiano:
-Igualdad de dos vectores:
se dice que dos vectores A y B son iguales si solo si A = B y A y B apuntan en la misma dirección a lo largo de líneas paralelas. Veamos en las figura que todos los vectores son iguales, lo único que cambia son sus puntos de inicio. Lo que nos permite mover un vector en un diagrama sin afectar las propiedades del vector.-Suma de vectores
: Para sumar vectores existe una regla geométrica llamada “El método del triángulo” (que aunque parezca mentira… se inventó antes de que naciera Jesucristo… lleva muchos pero muchos años funcionando). Este método consiste en dibujar los vectores desde el mismo punto de origen, el vector que une las puntas partiendo del primer elemento es en efecto el vector “suma”. Gráficamente es:
La suma de vectores es conmutativa, "A + B = B + A", si son tres a mas vectores, solo se deben agrupar (ley asociativa). Veamos la prueba geométrica de esta regla:

La suma de vectores también es asociativa "(A + B) + C = A + (B + C)". Para poder sumar vectores o asociarlos estos deben tener las mismas unidades. Es decir, no podemos sumar un vector velocidad con un vector aceleración. Cosa que entenderemos mejor a medida que avancemos en el curso. Veamos la demostración geométrica de la ley asociativa:

-Negativo de un vector:
Definimos el negativo de un vector A cualquiera, como el vector que sumado a A el resultado sea cero. Es decir, "A + (-A) = 0". El vector A y –A poseen la misma magnitud, el mismo sentido (están contenidos en la misma recta) pero direcciones opuestas.-Resta de vectores:
La resta de vectores es igual a la suma usando esta vez la definición del negativo de un vector. Definimos la operación A – B como A + (-B). Para realizar esta operación geométricamente tenemos dos caminos. 1) Dibujar el vector –B desde la punta del vector A entonces el vector que une la cola de A con la punta de B es el vector resta A – B. 2) Igual que en la suma, dibujar ambos vectores desde un mismo origen, el vector que parte del segundo elemento hacia el primero es el vector resta A – B. Gráficamente seria:
-Multiplicación por un escalar:
Si un vector A es multiplicado por un escalar “m”, dicho escalar aumentara la magnitud del vector A y en caso de ser negativo cambiará su dirección. La multiplicación por un escalar no afecta el sentido del vector.Componentes de un Vector y Vectores Unitarios:

Componentes de un Vector:
Un vector A puede ser expresado en función de sus proyecciones sobre los ejes coordenados X e Y como lo vemos en la figura, a esto se le llama “descomponer el vector” y aquí es cuando se vuelve útil saber usar las coordenadas polares, ya que podemos obtener las proyecciones Ax y Ay a partir de A y theta y viceversa, esto es:

El signo de las componentes Ax y Ay depende del angulo theta.
Vectores unitarios
Otra forma de representar un vector A es en función de los vectores unitarios i, j, k (ortogonales entre sí, es decir, que el ángulo que hay entre ellos es igual a 90°) del eje cartesiano. Un vector unitario es un vector adimensional cuya magnitud es exactamente igual a uno.

Podemos expresar entonces un vector A como:


Con esta representación algebraica, podemos realizar las operaciones de suma y resta de la siguiente manera:

Representando el vector R en sus componentes X e Y tenemos:

Donde evidentemente:

Desde un punto de vista gráfico podemos observar:

Destaquemos algo muy importante, la suma se hace por componentes, es decir, componentes en i de A se suman con componentes en i de B y lo mismo para j. Y como decía mi profesor “Para sumar vectores recuerden lo siguiente: los niños con los niños y las niñas con las niñas”.
Producto punto o producto escalar de vectores
Sean A y B dos vectores cualesquiera (con esto quiero decir que los valores de sus coordenadas, pueden ser cualquier número ) se define el producto escalar, como la multiplicación de sus componentes para cada eje coordenado, es decir, multiplicamos las componentes i con las i, las j con las j y las k con las k.
La proyección del coseno de un vector se define como
Cuando los vectores están escritos en su forma polar, esto es, que poseemos la magnitud y un angulo, entonces podemos calcular el producto escalar también llamado producto punto como “ el producto de los módulos de cada vector, multiplicado por el coseno del angulo que hay entre ellos ” .
el producto escalar o producto punto de vectores siempre tiene como resultado un número
El producto punto es una magnitud, por eso el resultado es un valor escalar, es decir, un número.
Producto vectorial o producto cruz vectores
Antes de comenzar a explicar, hay que aclarar un par de cosas,
El producto cruz de vectores solo está definido para tres dimensiones
No se puede realizar el producto cruz entre vectores que solo tienen dimensiones en el eje X e Y, si te fijas, un vector A = Ax j + Az k tiene 3 dimensiones solo que la componente Y vale cero y por eso no se escribe.
Ahora podemos continuar, el producto cruz entre dos vectores es un arreglo de tres, sí, de tres. El primero es el vector unitario u = i + j + k y luego los vectores que estamos por multiplicar A = Ax j + Az k , B = Bx i + By j + Bz k. Quedando de la siguiente forma:
Los signos del resultado son + - + si estás multiplicando 3 vectores recuerda seguir alternando el signo como + - + - . Pero en ese caso lo mejor es que realices primero un producto vectorial. Obtengas el vector resultado y lo multipliques por el siguiente.
El producto vectorial o producto cruz entre vectores siempre tiene como resultado un vector
Por eso se llama producto vectorial, el resultado es siempre un vector. Este vector tiene la particularidad de ser ortogonal al plano donde se encuentran los vectores que fueron multiplicados.
Producto vectorial mixto de vectores o producto triple de vectores
Sean tres vectores cualquiera A = Ax j + Az k , B = Bx i + By j + Bz k y C = Cx i + Cy j + Cz k. Se define el producto vectorial mixto como:
Este producto es fácil de recordar, solo tienes que correr hacia delante el ultimo vector para obtener la siguiente permutación, para desarrollarlo (en caso de que te pidan hacerlo, generalmente solo se usa la propiedad de permutación ) debes hacer el producto cruz y el resultado le haces el producto escalar.
Recuerda, como la ultima operación es un producto escalar, el resultado de este producto mixto es un valor cualquiera, es decir, un número.
Producto vectorial triple o producto vectorial entre tres vectores
Sean tres vectores cualquiera A = Ax j + Az k , B = Bx i + By j + Bz k y C = Cx i + Cy j + Cz k. Se define el producto vectorial triple como:
Esta propiedad, puede parecer difícil de recordar a primera vista, pero una nemotecnia que me sirvió a mi por muchos años fue BAC menos CAB así siempre la recordé y nunca fallé. Ten presente que el resultado del triple producto vectorial es un vector.
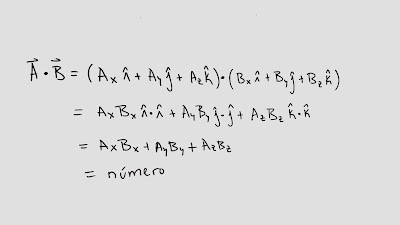
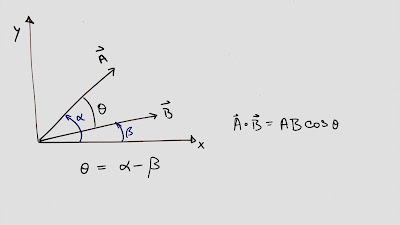


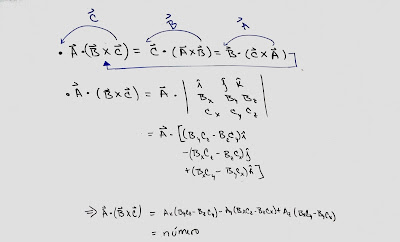




Comentarios
Publicar un comentario